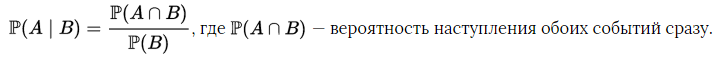Статистика

Статистика — отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных; изучение количественной стороны массовых общественных явлений в числовой форме.

Описательная статистика

Основные статистические показатели можно разделить на две группы:

• Меры среднего уровня дают усредненную характеристику совокупности объектов по определенному признаку
  • Среднее значение
  • Стандартная ошибка
  • Стандартное отклонение
  • Эксцесс
  • Асимметрия
  • Интервал
  • Минимум
  • Максимум
  • Счёт
  • Медиана
  • Мода
  • Квантиль
  • Математическое ожидание
  • Доверительный интервал
• Меры рассеяния показывают, насколько хорошо данные значения представляют данную совокупность
  • Дисперсия случайной величины
  • Среднеквадратическое отклонение
  • Размах вариации
  • Интерквантильный размах
  • Среднее абсолютное отклонение

Математическая статистика

• Функция правдоподобия - совместное распределение выборки из параметрического распределения, рассматриваемое как функция параметра. При этом используется совместная функция плотности (в случае выборки из непрерывного распределения) либо совместная вероятность (в случае выборки из дискретного распределения), вычисленные для данных выборочных значений.
• Экспоненциальные распределения - семейство функций распределения, включающих экспоненциальные члены. В качестве частных случаев содержит наиболее важные типы распределений, встречающиеся в реальных задачах (в том числе нормальное или гауссово распределение, альфа- и бета-распределения).

Статистический вывод

см. Статистический вывод

Статистические методы

• Регрессионный анализ (Regression analysis)
  • Outline of regression analysis - Techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables
  • Analysis of variance (ANOVA)
  • General linear model
  • Generalized linear model
• Оценка плотности (Density estimation)
  • Kernel density estimation
  • Multivariate kernel density estimation
• Временные ряды (Time series)
  • Time series Analysis
  • Box–Jenkins
  • Frequency domain
  • Time domain
• Мультивариантный анализ (Multivariate analysis)
  • Метод главных компонент (Principal component analysis, PCA) - один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации.
  • Факторный анализ (Factor analysis) — многомерный метод, применяемый для изучения взаимосвязей между значениями переменных. Предполагается, что известные переменные зависят от меньшего количества неизвестных переменных и случайной ошибки.
  • Кластерный анализ (Сluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы
• Робастность (Robust statistics) — метод, направленный на выявление выбросов, снижение их влияния или исключение их из выборки.

Теория вероятностей

• Случайное событие (событие) — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.
• Вероятность — степень (относительная мера, количественная оценка) возможности наступления некоторого события.
• Условная вероятность — вероятность наступления одного события при условии, что другое событие уже произошло.

  

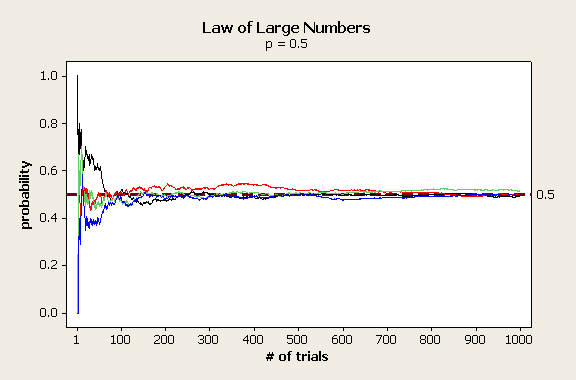
• Закон больших чисел: эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают:
  • слабый закон больших чисел, когда имеет место сходимость по вероятности;
  • усиленный закон больших чисел, когда имеет место сходимость почти всюду.

  

• Центральная предельная теорема - класс теорем, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Ссылки

• Введение в статистику и теорию вероятностей